

































相關專欄
書活網特推
葉丙成教授受邀TED演講,讓學生「沉迷於學習」的課程!驚艷與笑聲不斷!
離開校園的你,最懷念的一門課是什麼?
以前曾修過一門課,教材是《新世紀福音戰士》和《攻殼機動隊》兩部動畫,不過完全不輕鬆:課堂上除了要從各種角度剖析文本、援引相關理論形成論述,還有至少一萬字的期末報告。但畢業多年後,我對那門課仍記憶猶新。
為什麼?我想那是我第一次體會到「學問是活的」,它可以和生活如此靠近;當然,也是第一次了解到「跨領域研究」的困難之處。
看到《葉丙成的機率驚豔》的初稿時,我也有類似的感覺:好活的學問!也才知道,原來這是葉丙成老師的教學創舉,他的目的,正是讓學生找回自己的學習動機,讓學生成為學習的主體,而不再只是被動接收知識。
設計題目並不是簡單的事,更何況是把題目寫成一篇故事!寫出這些文章的,還是大家印象中和文學絕緣的理工科學生!不論是取材自影視或文學作品,還是直接從生活中擷取靈感,作者們的創意簡直令人嘆為觀止。與其說在文章裡加入算式,不如說他們在熟悉相關定理後,把生活裡隨處可見的機率,以數學方式萃取出來。
「驚豔」是我們對書名的一點堅持。不管對機率是否熟悉,我們仍相信所有人都可以從中看到學習的新方向和可能性,也都會為本書感到驚豔;一如我初見它時,心裡的那份喜悅。(/林雅萩)
內容簡介
博客來冠軍書!瞬間吸引數萬人報名!全球知名網站Coursera第一批華語課程
臺大電機系師生的「機率創意遊戲」,首度精華呈現!
Andrew Ng(《時代雜誌》百大最具影響力人物、全球最大線上教育平臺Coursera創辦人、史丹福大學副教授)、
洪萬生(前臺灣師範大學數學系教授)、單維彰(中央大學數學系教授)、鄭國威(PanSci泛科學網總編輯) 驚豔推薦
村上春樹筆下那對100% 的男女,分開後男孩再想起女孩是自己100% 伴侶的機率有多少?
如果印第安納.瓊斯走進《全面啟動》的夢境,全身而退的勝算有多少?
看Coursera人氣教授葉丙成如何引發學生最大潛能!
26篇來自臺大電機系、結合文學與數學的師生聯合創作,
讓你了解機率真的沒有想像中那麼難,而且超好玩!
這樣的老師這樣的課,不上實在太可惜!
.他是有史以來第一個在國際舞臺(Coursera)以華語對萬人講學、互動的老師。
.他是臺灣第一個設計體驗式簡報教學法,讓小學生打大學生期末簡報分數的老師。
.他是世界第一個將大規模開放式線上課程(MOOC)變成多人線上競技遊戲的老師。
.他是當代第一個推行「緣源流機率文學創作」的老師。
.對了,他……也是第一個綁馬尾見校長的臺大電機系老師……
一場線上學習新革命,看見未來教育新契機!
葉丙成,進入臺大教書五年後,即得到「教學傑出獎」,但他發現:「如果學生對這門課沒有學習動機,講得再有趣,也是對牛彈琴。」因此他思考如何把生活中遇到的問題數學化,透過數學的方式解答,並帶著學生重新定義學習,讓學生分組出題、互相測驗,以課程結合線上遊戲競賽的方式,讓學生真正沉迷在學習當中!
本書就像「紙上機率教室」,驚豔題目搶先玩!
.滿壘滿球數,外加兩人出局的情況下,投手該不該保送眼前的強打?
.當薛丁格打開下一個箱子,貓咪是死是活的機率有多少?
.各系舉辦的晚會都好精彩,該選哪一場,才不用排隊排很久?
.妙麗最後的遺言,是魔法?還是奇蹟?
.想在期末報告的夾縫中帶女朋友出去玩,最多可以去幾天?
*同時收錄葉丙成老師「機率與統計」課程的期中、期末考題,邀您一起try try看!
作者簡介
葉丙成
 號丙紳,現任臺大電機系副教授、臺大MOOC計畫執行長。自幼觀父葉勝年教授對生徒之關懷,而立後受臺大電機許博文老師「教授稱謂實不如師,多未傳道、解惑故」之啟發,輔以天生雞婆性格,漸步上熱血教師一途。
號丙紳,現任臺大電機系副教授、臺大MOOC計畫執行長。自幼觀父葉勝年教授對生徒之關懷,而立後受臺大電機許博文老師「教授稱謂實不如師,多未傳道、解惑故」之啟發,輔以天生雞婆性格,漸步上熱血教師一途。
其為師也,富熱情,常難忍教學一成不變。時於臉書輔導學子求學、人生之惑,後撰文部落格以惠同惑者,傳閱者眾。庚寅年某月見某生於課堂度孤,當夜不能寐。翻滾至五更,幡然悟得「by the students, for the students, of the students」之心法。自此教學通脫不拘,大開大闔,開發各式獨特教學法。教學深具特色,多有口碑,其簡報與表達課程收徒四十,初選常達數百眾。
其教學創舉無數,備受學生喜愛,並且樂於和學生一起享受創意的樂趣。
部落格「丙紳隨筆」:pcyeh.blog.ntu.edu.tw
臉書專頁:facebook.com/prof.yeh
賴以威
 數學專欄作家,師大附中,台大電機畢,現職中研院博士後研究員。認為如同語言的語感、音樂的音感,希望能透過寫作培養更多人的「數學感」。數學不枯燥,枯燥的是計算過程,數學不討厭,討厭的是考卷上的分數。信奉數學大師約翰•馮•諾伊曼的名言「If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is」。作品常見於聯合報《閱讀數學》、泛科學(Pansci)、有物報告、CAREhER等網路媒體,著有散文集《再見,爸爸》。
數學專欄作家,師大附中,台大電機畢,現職中研院博士後研究員。認為如同語言的語感、音樂的音感,希望能透過寫作培養更多人的「數學感」。數學不枯燥,枯燥的是計算過程,數學不討厭,討厭的是考卷上的分數。信奉數學大師約翰•馮•諾伊曼的名言「If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is」。作品常見於聯合報《閱讀數學》、泛科學(Pansci)、有物報告、CAREhER等網路媒體,著有散文集《再見,爸爸》。
個人臉書:https://www.facebook.com/iweilai0924
共同創作
黃大珉、蕭樂山、陳威宇、謝瑞賢、鄭子宇、朱柏憲、陳鴻猷、柯劭珩 等人
鄭子宇部落格「定理至此證畢」:qed314159.pixnet.net/blog
朱柏憲部落格「灑墨莊」:stegben.blogspot.tw/
得獎紀錄
★博客來自然科普類No.1
規格
ISBN:9789861371832
272頁,25開,西翻,平裝
目錄
推薦序
作者序 For the Student, By the Student, Of the Student!
作者序 紙上的電機之夜
初階
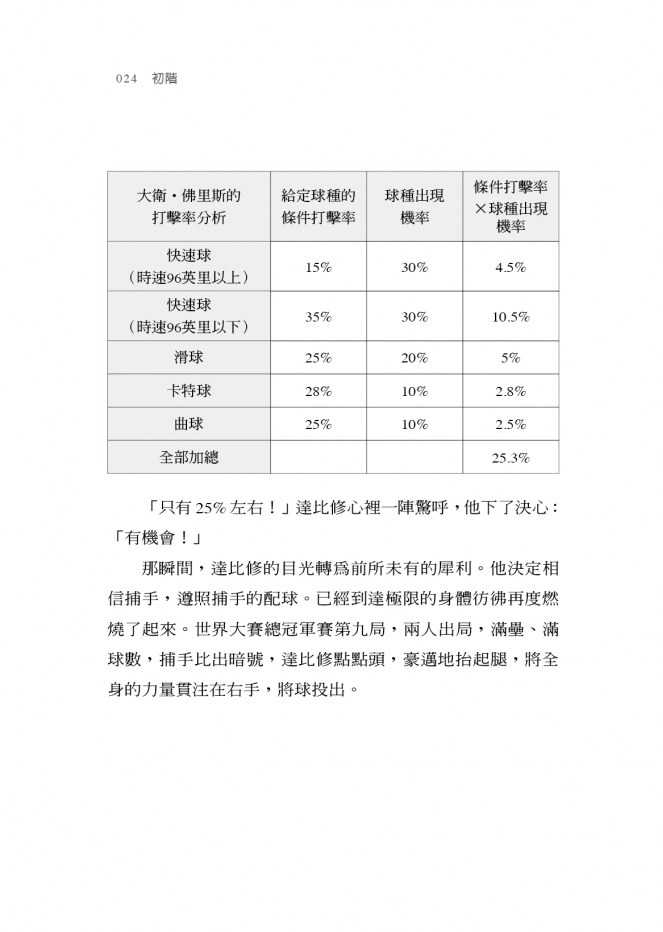
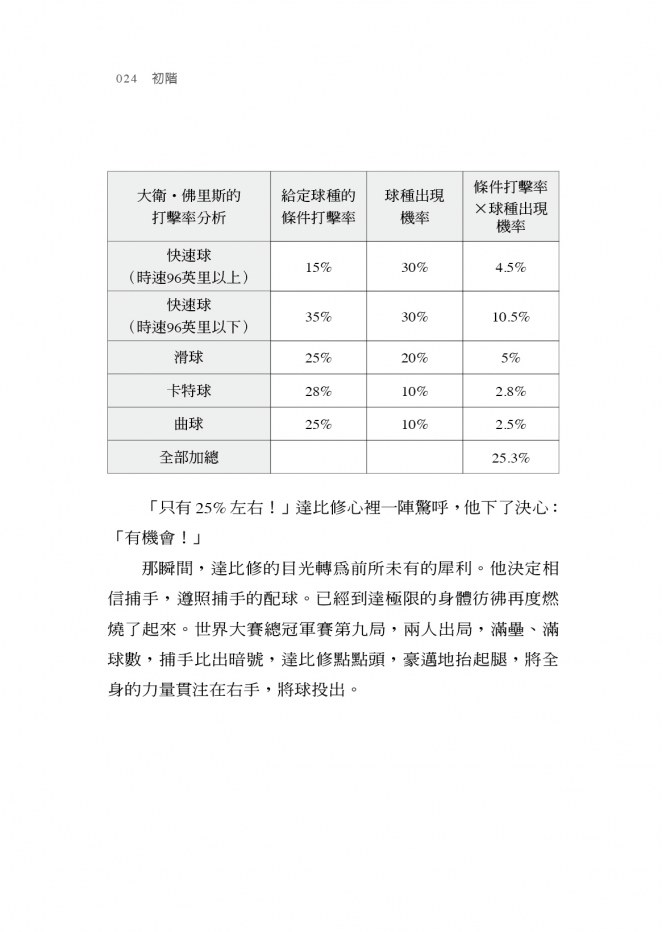
投手的兩難
現在,很想見你
有機農作物
熱愛冒險,才是真男人
近似完美句
Face on Fire!
薛丁格的貓咪日記
伊伊港載貨
生死一線間
少年郎的富翁漂流
角度,很重要
在進入下一個階段之前……
機率的意義
隨機變數及其函數
各種機率分布
中階
真實冒險
一戳就是快樂
阿母,不要摔我手機!
幾點去排隊?
巧克力拉霸
來顆晶體吧!
BJ4 online
V城追殺錄
Ramdomo
高階
大熊的高斯人生
格蘭傑的遺囑
男大學生的日常
在街角等待的 100%女孩
良不良,有關係
艾波寧的結局
附錄:葉丙成老師「機率與統計」課程期中、期末考題
期中考題
期末考題──瓊博的奇幻旅程
各界推薦
〈推薦序〉 Prof Andrew Ng(《時代雜誌》百大最具影響力人物、全球最大線上教育平臺Coursera創辦人、史丹福大學副教授)
葉丙成老師的這本書彰顯了教授數學的新方法。我認為對學生來說,這將會為他們帶來莫大的樂趣。
〈推薦序〉樂趣,加倍奉還 鄭國威(PanSci泛科學網總編輯)
「這不太可能吧?」
「這機會很大!」
「你有多少把握?」
我們每天都面臨機率問題,但我們每天都隨隨便便地應對,畢竟人生就是一團混沌,未來總是晦澀不明。然而葉丙成教授跟每一篇妙趣橫生的文章作者,以高度鬥智又逗趣的方式,將機率融入生活、時事、歷史,讓我佩服不已。還有什麼比用自己的文采與智慧出題考倒同學更爽快的?旁觀者如我,也不禁一會兒自我代入出題者,一會兒又代入解題者的角色,雖然總是被徹底考倒,但還是覺得好滿足,因為出題者是那麼認真。
看完這本書,雖然駑鈍如我還沒辦法躍身成為機率大師,但對於生活中每天都要面對的機率判斷,思緒好像變得清晰了點。本書中的「梗」多到數不清,除了能跟上年輕人的話題,還能長知識,可說一兼二顧,收穫多多。數學還是很難,但本書會將樂趣加倍奉還!
序
For the Student, By the Student, Of the Student!
還記得三年前某日,我在臺大電機系必修課「機率與統計」班上跟大家說:「有一天,我們一定會出版一本書,讓這個世界看到你們超級精采的創作才華!」三年後的今天,我們終於做到了!
這一切,源自於四年前我所開始的一場教學創新實驗。
我的教學生涯始於二○○一年。那一年,我開始在密西根大學當助教教課。從二○○一到二○一○的這十年中,我一直認為,教書就是要教得清楚、教得有趣。因此,我的教學理念就是追求「Be clear, Be fun」。直到二○一○年,我僥倖得到臺大的教學傑出獎。歷年獲獎的都是臺大在教學上素負盛名的前輩們。能與這些前輩齊名,對我是很大的鼓勵!
那時開始,我似乎有了一種錯覺:就像武俠小說一樣,覺得自己的教學似乎……已臻化境?頒完獎後的隔兩天,我在教室上課。當天我依然使出渾身解數,盡可能把課上得清楚、上得有趣。可是,我不由得注意到,在後排有三四位同學,一直在度估打瞌睡。等等,不是教學已臻化境?怎麼還會有人度估?以前上課的時候,即使學生度估也不以為意,但現在看到那些度估的人,卻很像一旦不小心看到液晶螢幕的亮點,就會忍不住老是往那裡看一樣。那一天,那些上課度估的人一直進入我的眼簾。我心裡不斷在想:「怎麼會有人度估?已經教的很清楚、很有趣,怎麼還會有人度估?」
直到當天晚上入睡時,這樣的疑惑依舊占據我腦海,甚至因此輾轉難眠。苦思到半夜,才突然想到:「原來他們就是沒有學習動機啊!」對於沒有學習動機的學生而言,老師教得再清楚、再有趣,他也不會想聽。以前我以為只要教得清楚有趣,學生自然就會有動機聽課。其實不是這樣的啊!
該怎麼做,才能燃起學生的動機?該怎麼做,才能讓他的動機熱烈持續一整個學期?這些才是教學能否成功的關鍵!在那當下,我才驚覺自己在教學上的道行實在太淺。想到自己竟曾生起「已臻化境」的念頭,不禁冒了一身冷汗!感謝四年前在我課堂度估的同學們,是他們點醒了我,讓我的教學理念從此改變!從那一夜起,我在教學上開始追求「如何讓學生維持學習動機」。
究竟該怎麼做,才能引起學生的學習動機呢?這個問題一直苦惱著我。恰好在同一個時間,我也被另一個問題苦惱著:「如何解決常見的作業抄襲問題?」
根據我去臺灣各地演講訪查的結果,發現臺灣大學生的作業抄襲問題非常嚴重。學生抄作業固然不對,但也有其背後的原因。主要是大學生修習的學分太多了,一學期修二十幾個學分,八、九門課,遠比美國大學生只有四、五門課多很多。一學期修八、九門課,讓學生根本沒有時間好好思考,更別說把作業好好磨出來。如果一個題目花了兩三分鐘還做不出來,很多人就會去看習題解答。因為有那麼多科目都要顧,沒辦法單單只在某科的某題作業冒險花那麼多時間,所以學生或是抄襲直屬學長學姐過去留下來的作業答案(學生稱之為「家產」),或是抄襲班上同學的答案,或是抄襲學校旁影印店所賣的各科教科書習題解答……作業的抄襲,是臺灣非常嚴重的問題。
那麼,該如何解決呢?我想到了一石二鳥的方法!我決定把作業變成一種多人線上遊戲。每教完一個章節,我就讓學生自己設計作業題目,然後互相攻破別人的題目。攻破越多題目的人,在地圖上就越領先其他人。由於題目都是每組學生自己設計的,同學就想抄答案也沒得抄,只能被迫好好去思考如何按部就班解出別人的題目!非常感謝我的研究生姜哲雄和唐偉軒,他們以優異的程式設計能力,將這個多人線上遊戲平臺建構出來。在二○一一年下學期,我們的系統正式上線,名字就叫做「BJT-Online」!(細節詳見:pcyeh.blog.ntu.edu.tw/archives/135)
「BJT-Online」這個出題互解的線上遊戲,一方面因為有遊戲元素,使得學生非常投入,另外一方面也因為是靠學生自己出題,所以學生花了更多時間研讀課本內容,期能找出好的材料來設計好的題目。另外,我也發現,透過自己設計題目的經驗,學生們對於題目隱藏架構的洞察力和解題能力,都有顯著提升!
此外,對於數學教育,我一直有自己的堅持:「學生學會以後要會用!」我發現很多學生看到變成數學式子的問題後,都很會解題。但若是在生活或是研究中碰到實際問題,卻有很多人不會利用數學來解。為什麼呢?主要的原因在於:學生看得懂數學式子與數學語言,但日常生活所碰到的問題,卻往往是以「人」的語言來描述的。很多學生欠缺將「人的語言」轉譯成「數學語言」的能力,以至於碰到實際問題時,無法運用所學的數學知識來解決這些問題。
因此,我出的機率考試題目,每年都是很變態的(笑)、滿滿三大頁全是字的應用題,鮮少出現數學式子。學生往往戲稱寫我的題目,簡直就像是在考閱讀測驗一樣!每年考題都是以印第安納.瓊斯博士為主題,設計出揉合故事與數學的題目。我的目的就是要從中磨練學生應用數學於實際問題的能力。另外,由於題目都相當有故事性、趣味性,常常在考場中看到學生一邊解題,一邊莞爾偷笑的景象。我的理念就是「讓學生考不好也會笑!」我希望讓學生即使考不好,也還是對這門科目留下好印象。他日若因其他原因必須重拾這方面的學問時,相信這些學生也比較能再燃起對這一科的學習熱情。
由於我都是出這類型的題目,因此同學們出的作業題也有著類似的風格。這些年來,臺大電機同學們的創作能力,每每讓我驚嘆!大家設計的機率題目揉合了數學與各式各樣的故事:有以《悲慘世界》入題的,也有以葉問入題的;有以村上春樹入題的,也有拿《哈利波特》同人誌入題的。臺大電機同學們驚人的創意作品,往往讓我拍案叫絕!由於學生出題的繳交期限多是半夜三點(ㄟ……不是我變態,是配合學生們的作息啦 @@)。我常常在半夜三點窩在床上,用平板上網看學生出的題目,每次都忍俊不住,邊看邊哈哈大笑。在旁早已入眠的內人,常常被我的笑聲吵醒,實在過意不去!(老婆!真的都是我的學生害的啦!)
這種讓學生出作業的教學方法,後來收到很大的成效。學習效果較我以往的傳統式教學進步很多,學習動機也有顯著提升。自從採用這種教學方法之後,我又衍生出許多新方法:讓學生評分、讓學生設計課程、讓學生決定學習步調等。這一系列教學方法中,都有我的新教學理念貫穿其中:「for the student, by the student, of the student!」
現今很多老師的教學理念都是「for the student, by the teacher, of the student (?).」往往是老師為了學生,辛辛苦苦地把一切東西都準備得好好的,替學生設計各式各樣的教材、作業、題目。一切的工作都是老師獨力在做,但為學生做了這麼多,卻常常得不到學生的肯定與回應,學生的學習效果也不如老師預期的好。為什麼呢?
箇中原因就在於:老師剝奪了學生學習的主動權,以至於學生失去了學習樂趣,也失去了學習動機。試想:若一個人每天都被別人硬塞大魚大肉,他對於吃還會有什麼欲望嗎?我們該做的,是讓學生餓!讓學生重拾學習的主動權!只要將老師平常握在手中的教學權力(出題、評分、授課),下放一部分給學生,學生就會覺得自己對學習有更多的主導權,他們對於學習也將更有動機、更有興趣!
老師,我們不需要再把自己搞得這麼累了!辛苦半天,卻像個不被感激的老媽子一樣,何必呢?不如給一點空間,放手讓學生胡搞瞎搞一陣!
For the student, by the student, of the student!
葉丙成 二○一四年一月
〈作者序〉紙上的電機之夜
嚴格說起來,這篇序言是我在本書中唯一的創作。
在編寫這本書的過程中,我所做的扮演的腳色只是,從累積好幾年的作業裡,挑出適合的作品,然後和其他作者們討論,一起將題目與解答改寫成一篇篇散文,試著讓那些就算提不起勁解題目的少數(多數?)讀者,也能享受閱讀的樂趣、感受到題目的創意,還有那理當跟作業完全扯不上關係的——「趣味」。
我們活在一個自由的時代,可以自己選擇就讀哪門科系、從事哪份職業,甚至連讓誰走進總統府,看起來都是我們說了算。但事實上,絕大多數的我們依然循規蹈矩,走在別人走過的路上。這樣的道路不見得不好,假如是經過時間淬煉的路徑,也就是所謂的「傳統」,那麼跟隨優良的傳統,可以避免不必要的錯誤嘗試。
然而,有些時候因為習慣,因為「好像大家都這麼做、這麼想」,所以我們一不小心,即將一些事情或行為視為理所當然。
這本書想傳遞的就是一些「其實不一定這樣」的想法。
出題比解題學得更多
我的指導教授教導我,做研究最重要的就是不要「因為書本或論文這麼寫,所以這麼做」,幾千年前也有一位老師說過「盡信書,不如無書」。對每件事都抱持著懷疑的心態、親自嘗試,直到發現能說服自己的理由,才真正接受這件事。這是我在念研究所時,親身體驗、學到最寶貴的一課。試想:
把思考的責任交給素未謀面的人,不是一件不負責任的事嗎?
雖然沒有問過葉老師,但我想他必定也將這樣的研究精神應用在他熱愛的教育之中,仔細檢驗課堂中的每一個步驟。
「嗯,為什麼一定要由老師出題,而不讓學生彼此之間出題競爭呢?」
這個念頭彷彿一顆種子,而這本書則是種子發芽、茁壯後,開出的一朵花。
葉老師開這門機率課時,我已經畢業很多年了(面不改色摸摸魚尾紋)。
知道他用這種方式,要求學生互相出題考對方後,我想像了一下:如果是大學時代的我,恐怕也會一不小心就誤入陷阱,或是努力出題設計同學。教過人、站在學習的另一端體驗過的人都知道,從講解或出題過程中所學到的東西,絕對比解題更多。解題只要將出題者發過來的球打回去就可以,但出題卻必須了解所有知識,才知道該如何設計題目、如何發出一記難接卻有意義的球。
理工人的文字舞臺
我很享受整理這本書的過程。
書中有些文章融合了大學生活與數學機率。閱讀時,文字彷彿像夜市裡的夾娃娃機,一把伸進大腦的深處,將青春的尾巴和大學回憶,一個個鉤出來。大學晚會、圖書館念書、新生入學前總期待自己能收到學妹,新生入學後第一天,忍不住把失望的怒氣發洩在學弟身上。這些事情我都做過(對不起,學弟)。
除此之外,還有許多文章的靈感源自於文學名著、電玩遊戲、熱門電影。這是一份集體創作,除了葉老師,還有一起合作的八位學弟:黃大珉、蕭樂山、陳威宇、謝瑞賢、鄭子宇、朱柏憲、陳鴻猷、柯劭珩,以及許多未曾謀面、修了這門機率課程的學弟妹們。在合作過程中,除了看見他們如何充滿創意地將生活中的數學元素萃取出來,剛滿二十歲的他們,對文字的掌握度與表達能力,更令我驚豔。
這讓我想起大學時,每系都有自己的晚會,系上同學能在晚會中盡情展現學業以外的才藝。以前我很喜歡去這種晚會(內文恰恰有一篇計算晚會排隊方式與入場機率的文章),除了能趁機對暗戀的學伴獻殷勤,也能看見朋友深藏不露的一面,那種感受總是很驚奇、很有趣。這本書的每一頁就是一片舞臺,讓出題的學弟妹們有機會在各位面前舞文弄墨。希望各位讀著讀著,會像參加大學系上晚會一樣感到驚喜,心中浮起「原來理工人也有這麼好的文筆」的感受。
左腦跟右腦,本來就是合作無間的,不是嗎?
無趣的不是數學,而是基本動作
此外,我私心把序言當作許願池,希望這本書能改變大家對數學的誤會──誤會數學總是無趣。
或許,這稱不上誤解,畢竟要是在街上隨機抽樣,十位路人中,大概有九位不僅會認為數學很無聊,還能說出許多充分理由,因為從七歲到十八歲,甚至到二十二歲大學畢業,再可憐一點的到二十四歲研究所畢業,我們多少都曾經遭受過數學的荼毒。
然而我認為,大多時候我們感受到的「無聊」並非數學本身,是關於數學的「基本動作」。
數學是一門累積了幾千年的學問,不像語言偶爾有例外──偶爾有不規則動詞、偶爾這樣用或那樣用都差不多。數學講究高度的精確與量化。學校義務教育的課程中,大部分練習的都只是數學的基本動作,就像打籃球要練習運球、上籃;念英文時要背單字和動詞時態;打桌球時要對牆打、揮空拍,這些也是籃球或英文或桌球的一部分,但跟我們想像中那種在球場奔馳、背著背包在國外自助旅行與外國人對話的感覺又不太一樣。
不論哪一門知識或技藝,基本動作練習都相當無聊。
不然《灌籃高手》裡的櫻木花道,就不會在前幾集裡整天抱怨自己只能在場邊彎腰運球。
為了熟練,我們必須硬生生地將數學與生活切割開來。翻開課本,只看見冷冰冰、宛如死去的數學基本動作。真正的數學隱藏在生活之中,隱藏在帳單、科技產業、電玩遊戲,還有各種更難以想像的地方。這本書或許有些地方太過浮誇、有些地方不切實際,又有些地方純屬搏君一笑。可是,我希望透過它,讓大家感受到數學的溫度,並且重新思考:
數學其實沒有這麼討厭、這麼惱人。
賴以威 二○一四年一月













